Go To Blogs

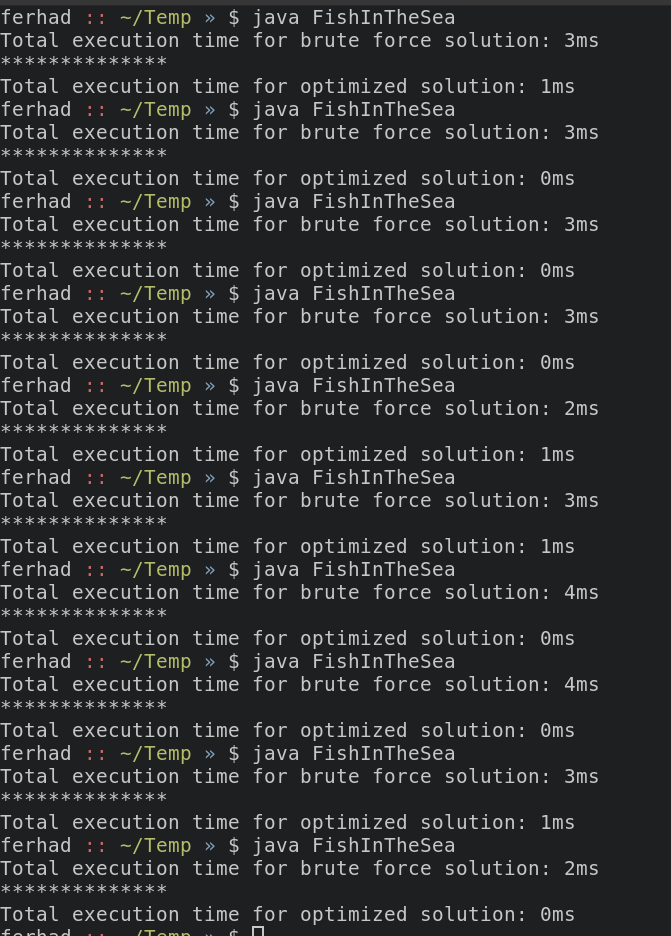
My optimized solution to Fishes in the Sea problem

Tags: Algorithms, Dynamic programming, Optimization, Memoization, Fishes in The Sea

Categories: algorithms

Date: 2021.09.26

Problem

Given a Sea in the middle of an ocean of n*m dimensions. Each field in this Sea contains a positive integer which is the amount of fishes that exist in that field. Initially the whale is at the first column but can be in any row. The whale can move only right (→), right-up (↗), right-down (↘) from any cell in the first column. Find out the maximum amount of fish it can collect.

Input/Output examples:

int matrix[][] = {
    {1, 3, 3},
    {2, 1, 4},
    {0, 6, 4}
};
// => 12
// (1, 0) → (2, 1) → (2, 2)

Table of contents

Foreword

I will take one of the example matrices and go through it to explain the steps:

int matrix[][] = {
    {1, 3, 1, 5},
    {2, 2, 4, 1},
    {5, 0, 2, 3},
    {0, 6, 1, 2}
};
// => 16
// (2, 0) → (1, 1) → (1, 2) → (0, 3)
// (2, 0) → (3, 1) → (2, 2) → (2, 3)

Recursive counting

If we think of this matrix as the sea, its elements as the number of fish in each field, and jumps between matrix elements as movement (right, right-up, right-down), we can represent it as a graph.

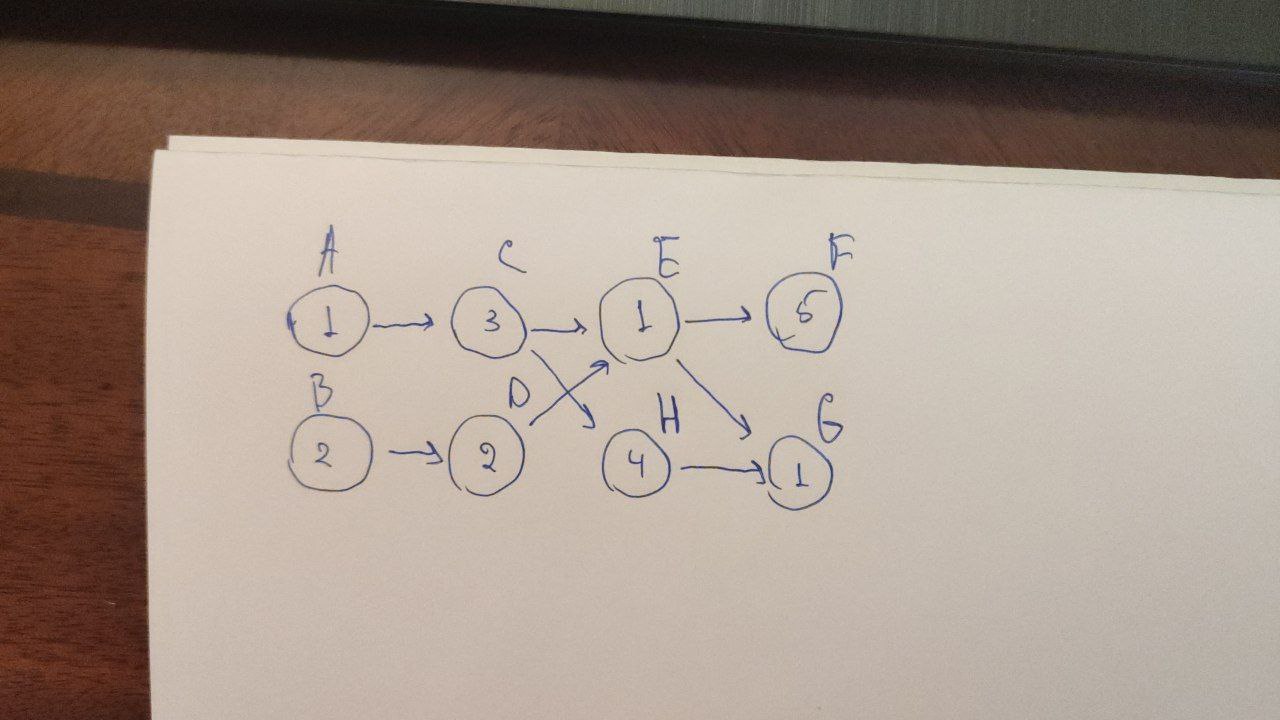
Matrix as Graph

Consider this image as the first two rows of the above matrix. Letters (A, C, E, F, B, D, H, G) are vertices and arrows (A → C, C → D, etc.) are edges of the graph. This graph representation allows us to use recursive counting to find:

  1. How many paths are required to traverse the entire graph?
  2. The maximum count of fish the whale can eat.

Recursive Counting

NOTE: In actual code, the algorithm works in reverse because of recursion (paths go from right to left instead of left to right). For clarity, it’s described here as left to right.

Each vertex has three attributes (left, value, right). For example, for element(0, 2):

left = 7
value = 1
right = 8

Where:

Brute force solution

The above approach is efficient, as we don’t need to revisit identical paths. For example, consider these paths:

element(0, 0) -> element(0, 1) -> element(0, 2) -> element(0, 3);
element(0, 0) -> element(0, 1) -> element(0, 2) -> element(1, 3);

These paths differ by only one vertex. Without memoization, the program would follow each path independently, resulting in brute force computation.

class FishesInTheSeaB {
    public int solve(int[][] matrix){
        int max = 0;
        for (int i = 0; i < matrix.length; i++) {
            int currentFish = maxFish(matrix, i, 0);
            if (currentFish > max) {
                max = currentFish;
            }
        }
        return max;
    }

    private int maxFish(int[][] matrix, int i, int j) {
        if (j >= matrix[0].length - 1) {
            return matrix[i][j];
        }
        int right = matrix[i][j] + maxFish(matrix, i, j + 1);
        if (i <= 0 || j >= matrix[0].length - 1) {
            return Math.max(right, matrix[i][j]);
        }
        int rightUp = matrix[i][j] + maxFish(matrix, i - 1, j + 1);
        if (i >= matrix.length - 1 || j >= matrix[0].length - 1) {
            return Math.max(rightUp, Math.max(right, matrix[i][j]));
        }
        int rightDown = matrix[i][j] + maxFish(matrix, i + 1, j + 1);
        int max = Math.max(rightDown, Math.max(rightUp, Math.max(right, matrix[i][j])));
        return max;
    }
}
Time Complexity: O(n) * O(3^m) = O(n*3^m)
Space Complexity: O(n)

Optimization. Memoization

With memoization, we can avoid recalculating paths, optimizing the program:

class FishesInTheSeaM {
    private int[][] memoization;

    public int solve(int[][] matrix){
        memoization = new int[matrix.length][matrix[0].length];
        int max = 0;
        for (int i = 0; i < matrix.length; i++) {
            int currentFish = maxFish(matrix, i, 0);
            if (currentFish > max) {
                max = currentFish;
            }
        }
        return max;
    }

    private int maxFish(int[][] matrix, int i, int j) {
        if (memoization[i][j] != 0) {
            return memoization[i][j];
        }
        if (j >= matrix[0].length - 1) {
            return matrix[i][j];
        }
        int right = matrix[i][j] + maxFish(matrix, i, j + 1);
        if (i <= 0 || j >= matrix[0].length - 1) {
            return Math.max(right, matrix[i][j]);
        }
        int rightUp = matrix[i][j] + maxFish(matrix, i - 1, j + 1);
        if (i >= matrix.length - 1 || j >= matrix[0].length - 1) {
            return Math.max(rightUp, Math.max(right, matrix[i][j]));
        }
        int rightDown = matrix[i][j] + maxFish(matrix, i + 1, j + 1);
        int max = Math.max(rightDown, Math.max(rightUp, Math.max(right, matrix[i][j])));
        memoization[i][j] = max;
        return max;
    }
}
Time Complexity: O(n) amortized
Space Complexity: O(n)

Benchmark

Benchmark